Student showcase in Mathematical Sciences 2021

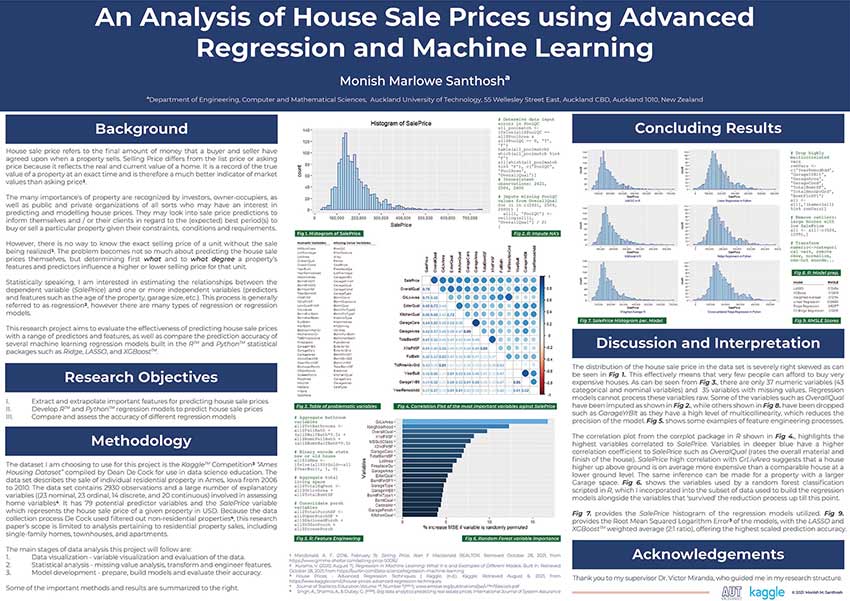
Data analysis and predictive analytics were performed on the Kaggle Competition 'Ames Housing Dataset'. Relationships between a residential property unit's house sale price and 79 various other predictors such as the age and garage size were explored and interpreted in R. Missing values analysis, variable imputations, categorical to numeric transformations (and vice versa), and feature engineering techniques were applied. Four regression and regression based machine learning techniques were built including simple linear regression, ridge regression, cross-validated ridge regression, LASSO and XGBoost in R and Python. The models’ prediction accuracy were then improved and commented on.

Project website (Kaggle)

Student(s)

• Monish Marlowe Santhosh
  Bachelor of Mathematical Sciences

Supervisor

• Dr. Victor Miranda

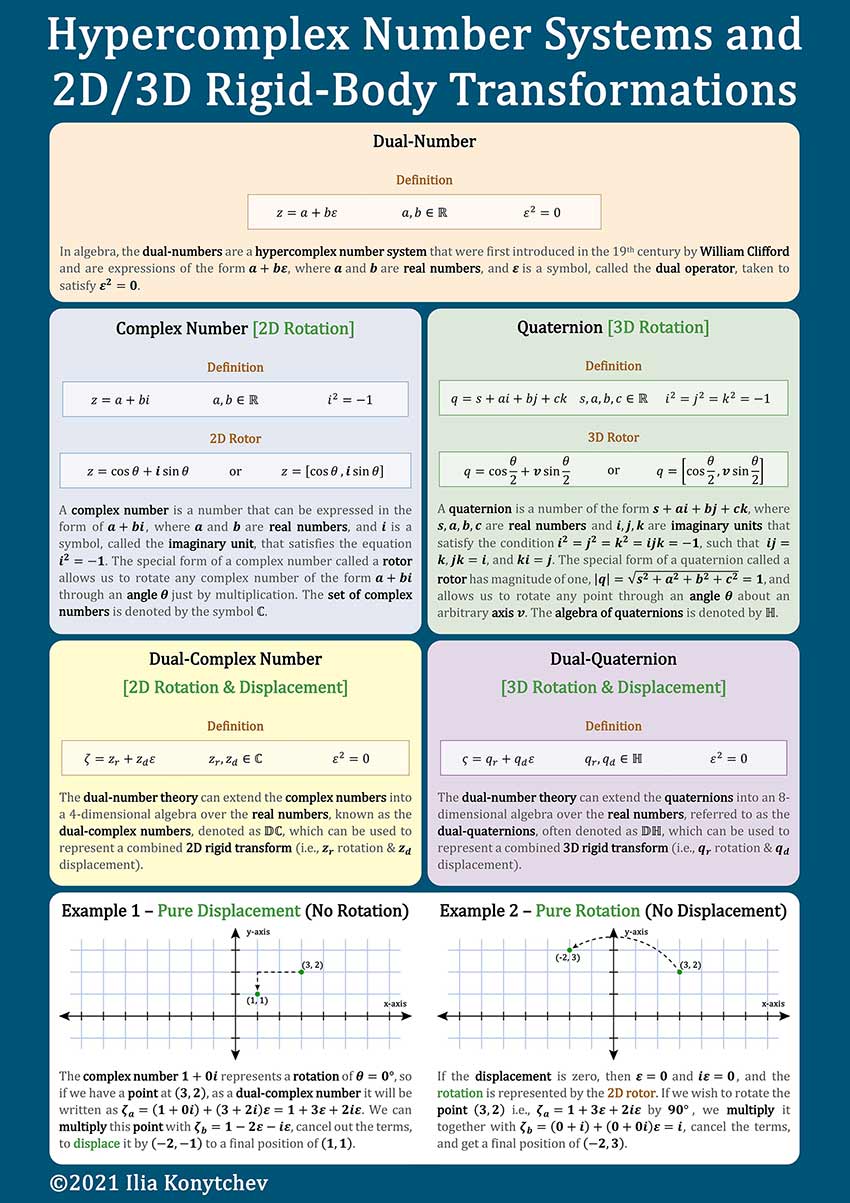
Studied the underlying principles of and performed a literature review of a mathematical construct known as a dual-quaternion, which is a special case of a biquaternion when the coefficients are dual-numbers instead of complex, or split-complex numbers. Similar to the way that rotations in 3-dimensional space can be represented by quaternions of unit length, rigid motions (i.e., combination of rotation and displacement) can be represented by dual-quaternions of unit length. The quaternions have found numerous applications outside of pure mathematics, especially in fields such as physics, robotics, and computer graphics due to their uncanny ability to describe orientations in 3-dimensional space without suffering from artifacts such as gimbal lock. Dual-quaternions on the other hand are less well studied, hence prompting this research to see if they offer similar advantages as quaternions as it pertains to 3D rigid-body transformations. The object of interest in particular was the 4x4 homogeneous transformation matrix, which is a traditional method used for performing linear transformations in 3d space, and a discussion and analysis of the two methods was performed.

Student(s)

• Ilia Konytchev
  Bachelor of Mathematical Sciences

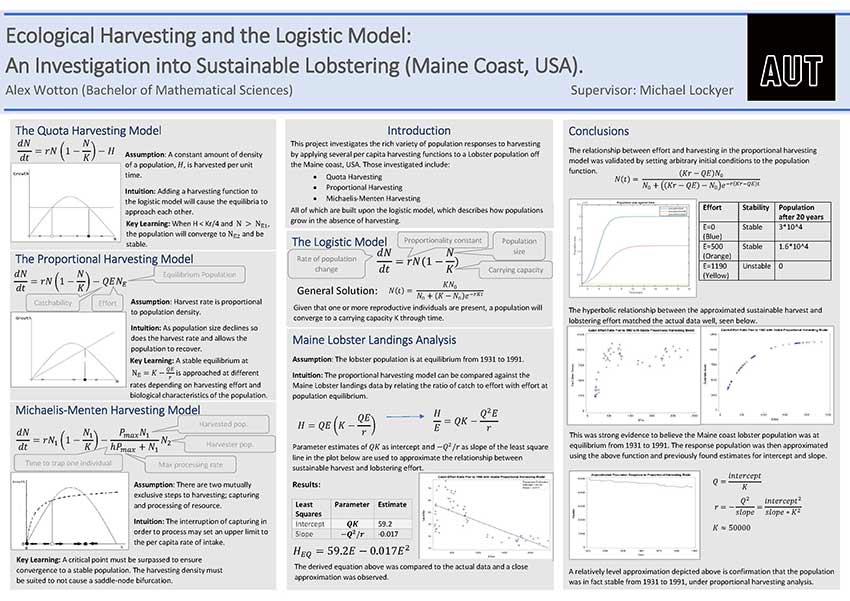
Economic wealth is latent in the resources of the natural world. Whether it be fishermen in a poor village raising themselves from poverty, or large oil companies dominating the petroleum market, common resources are exploited on all scales. In the context of fisheries, wealth generating continues until the harvest level reaches the maximum growth rate of the fish population. For every subsequent entry of a new fisher the fish population begins to decline and heads toward extinction unless a sufficient decrease in the number of fishers occurs. Significant advancement in technologies throughout the later part of the nineteenth century has enable sophisticated fishing fleets to crush global fish populations, to supply the world’s markets. The rich variety of population responses to harvesting are modelled by several per capita harvesting functions. All of which contain critical points where, if approached, small further increases in harvesting results in discontinuous and large changes to the population. Otherwise known as bifurcations, it can often be difficult or impossible to steer away from extinction when this harvesting phenomenon occurs. Exploring how ecological and human factors influence a populations stability enables careful and sustainable manipulation of population dynamics. A discussion of the effects of harvesting can arise in the analysis of a mathematical model of the growth of a population. Harvesting is a general term for the removal of members of a biological population. In addition to the factors of reproductive rates and competition for resources, we must consider the effect of harvesting on a populations growth rate. For the following analysis it is taken that in the absence of harvest, populations grow according to the logistic model. Most populations are constrained by limitations on resources such that, given a period of time, a populations growth rate will eventually decline to zero. Thus, a population, N, will always be less than its maximum supportable population, referred to as an environmental carrying capacity, K

Student(s)

• Alex Wotton
  Bachelor of Mathematical Sciences

Supervisor

• Michael Lockyer

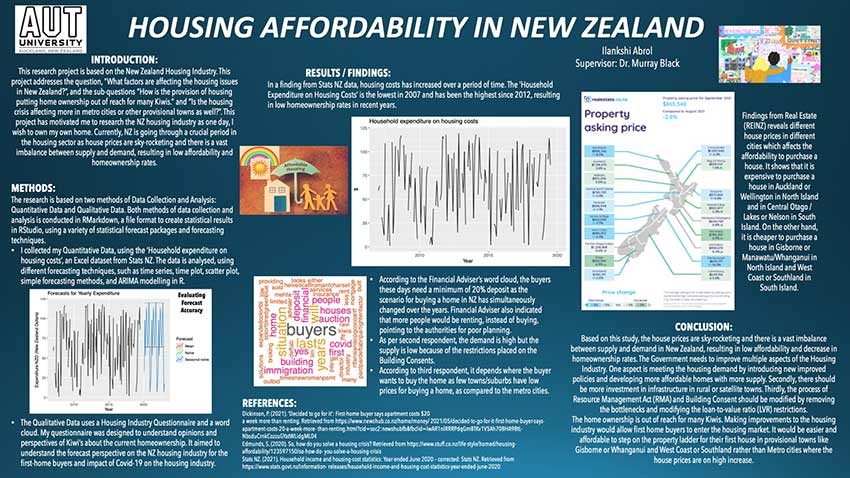
This research project is based on the NZ Housing Industry. This project addresses the question, “What factors are affecting the housing issues in NZ?”, and the sub-questions “How is the provision of housing putting home ownership out of reach for many Kiwis.” and “Is the housing crisis affecting more in metro cities or other provisional towns as well?”. Currently, NZ is going through a crucial period as house prices are sky-rocketing and there is a vast imbalance between supply and demand, resulting in low affordability for first home buyers and low homeownership rates. My research is based on two methods of data collection and analysis: quantitative data and qualitative data.

Student(s)

• Ilankshi Abrol
  Bachelor of Mathematical Sciences

Supervisor

• Dr. Murrary Black

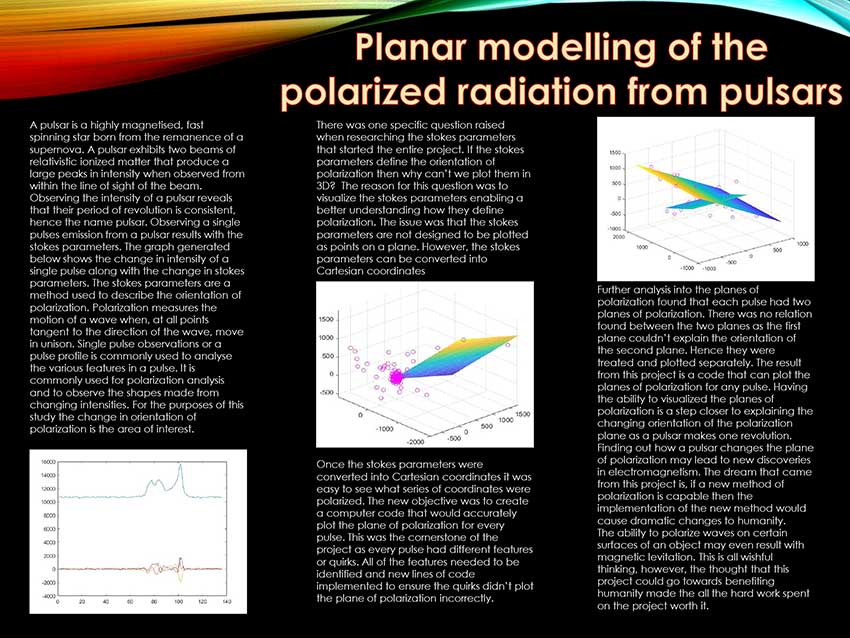
The Arecibo observatory observed data on pulsar B1919+21, The data observed was used within this paper to create a code that could model the planes of polarized radiation from the pulsar. Two planes of polarized radiation exist within each pulse, each pulse has huge degrees of variablility and many different features. The model can accurately locate and plot the polarized planes. The results show the orientation of the planes granting a visual representation of how the planes of polarized radiation change per pulse.

Student(s)

• Oliver Laycock
  Bachelor of Mathematical Sciences

Supervisor

• Willem Van Straten

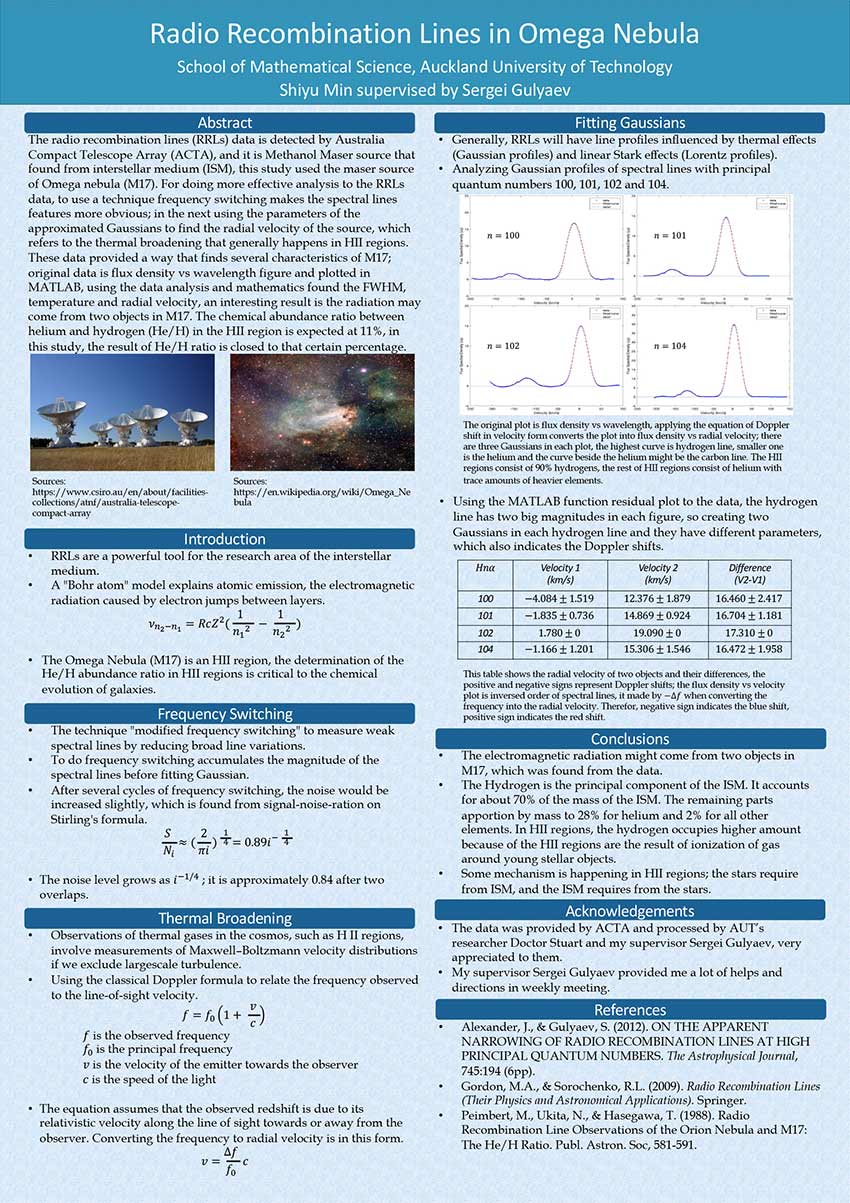
The spectral lines carry numerous information about the interstellar medium, we can find them through the analysis of radio recombination lines, it is a powerful tool in astrophisical reserch area. This project will provid the radial velocity, and magnitude of RRLs that come from Omega Nebula (M17), and more information were found from the spectral lines' features, such like temperature, chemical abundance and FWHM, data analysis and mathmatics are helpful to find these critical information.

Student(s)

• Shiyu Min
  Bachelor of Mathematical Sciences

Supervisor

• Sergei Gulyaev